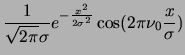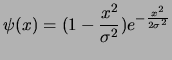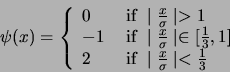[Home] [Book] [Publications] [Multiresolution] [MR/1]
1D Transforms :

1D Wavelets and Multiscale Transforms

19 transforms are implemented, which are grouped into 5 classes

Morlet, Mexican hat, and French hat wavelet transforms are non-dyadic (the resolution is not decreased by a factor two between two scales), and 12 voices (fixed value) are calculated (instead of one for the dyadic case) when the resolution is divided by two. Then the number of rows in the output image will be equal to 12* number_of_scales. The Morlet wavelet is complex, so the wavelet transform is complex too. Four transforms are non-redundant: the bi-orthogonal, the lifting scheme, and the wavelet packet methods (transforms 17 and 18). In this case, the output is not an image but a signal (i.e. 1D rather than 2D), which has the same size as the original one. For (bi-) orthogonal transforms (decimated and undecimated), the user can use its own filters.

  1. linear wavelet transform: à trous algorithm
  2. B$ _1$-spline wavelet transform: à trous algorithm
  3. B$ _3$-spline wavelet transform: à trous algorithm
  4. derivative of a B$ _3$-spline: à trous algorithm
  5. undecimated Haar wavelet transform: à trous algorithm
  6. morphological median transform
  7. undecimated (bi-) orthogonal wavelet transform (decimated and undecimated)
    1. Antonini 7/9 filters
    2. Daubechies filter 4
    3. Biorthogonal 2/6 Haar filters
    4. Biorthogonal 2/10 Haar filters
    5. Odegard 7/9 filters
    6. User's filters
  8. pyramidal linear wavelet transform
  9. pyramidal B$ _3$-spline wavelet transform
  10. pyramidal median transform
  11. Morlet's wavelet transform
    Continuous wavelet transform with a complex wavelet which can be decomposed into two parts, one for the real part, and the other for the imaginary part:
    $\displaystyle \psi_r(x)$ $\displaystyle =$ $\displaystyle \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{x^2}{2\sigma^2}} \cos(2\pi\nu_0 {x \over \sigma})$  
    $\displaystyle \psi_i(x)$ $\displaystyle =$ $\displaystyle \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{x^2}{2\sigma^2}} \sin(2\pi\nu_0 {x \over \sigma})$  

    First scale 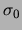$ \sigma_0$ is chosen equal to 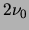$ 2 \nu_0$ and $ \nu_0 = 0.8$, using 12 voices per octave.
  12. Mexican hat wavelet transform
    Continuous wavelet transform with the Mexican hat wavelet. This is the second derivative of a Gaussian
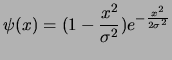    $\displaystyle \psi(x) = (1 - {x^2 \over \sigma^2}) e^{-\frac{ x^2}{2\sigma^2}}$     (1)

    First scale 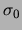$ \sigma_0$ is chosen equal to 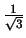$ {1 \over \sqrt{3}}$, using 12 voices per octave.
  13. French hat wavelet transform
    Continuous wavelet transform with the French hat wavelet
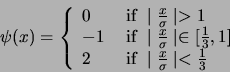    \begin{displaymath}\psi(x) = \left \{ \begin{array}{ll} 0 & \mbox{ if } \mid {x ... ...f } \mid {x \over \sigma} \mid < {1 \over 3} \end{array}\right.\end{displaymath}     (2)

    First scale 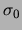$ \sigma_0$ equal to $ 0.66$, and 12 voices per octave.
  14. Gaussian derivative wavelet transform
    Continuous wavelet transform. The wavelet is the first derivative of a Gaussian
    $\displaystyle \psi(x) = - x e^{-\frac{1}{2}x^2}$     (3)

    First scale 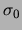$ \sigma_0$ equal to 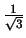$ {1 \over \sqrt{3}}$, and 12 voices per octave.
  15. (bi-) orthogonal transform.
    Implemented filters are
    1. Antonini 7/9 filters
    2. Daubechies filter 4
    3. Biorthogonal 2/6 Haar filters
    4. Biorthogonal 2/10 Haar filters
    5. Odegard 7/9 filters
    6. User's filters
  16. (bi-) orthogonal transform via lifting scheme.
    Implemented lifting scheme method are:
    1. CDF WT
    2. median prediction
    3. integer Haar WT
    4. integer CDF WT
    5. integer (4,2) interpolating transform
    6. 7/9 WT
    7. integer 7/9 WT
  17. Wavelet packets.
  18. Wavelet packets via lifting scheme.
  19. Wavelet packets using the à trous algorithm.